Maths
Children at Abacus THRIVE because they are problem solvers, challengers, critical thinkers, statisticians and financiers! They have a strong foundation of concepts and are able to make connections through their application of mathematics. They reason, generalise and make sense of mathematical problems and embrace opportunities to explore marvellous mistakes.
"When we get stuck in Maths, we keep trying and don’t give up! If you still need help, you can ask the teacher and they will show you again." - Reception pupil.
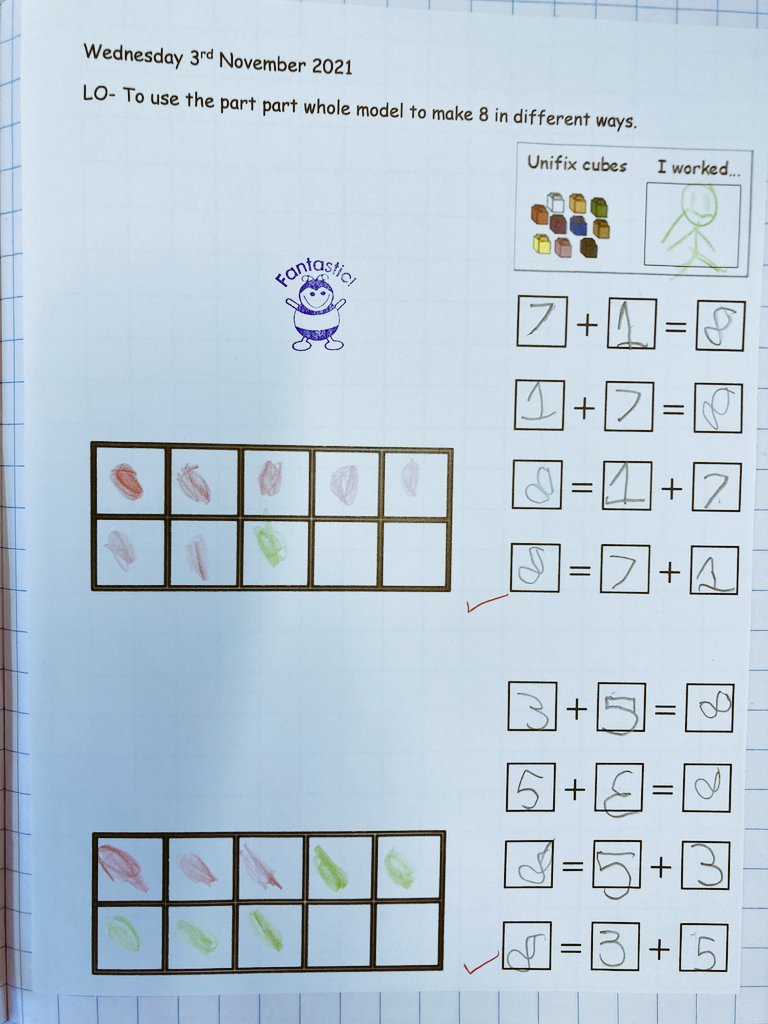
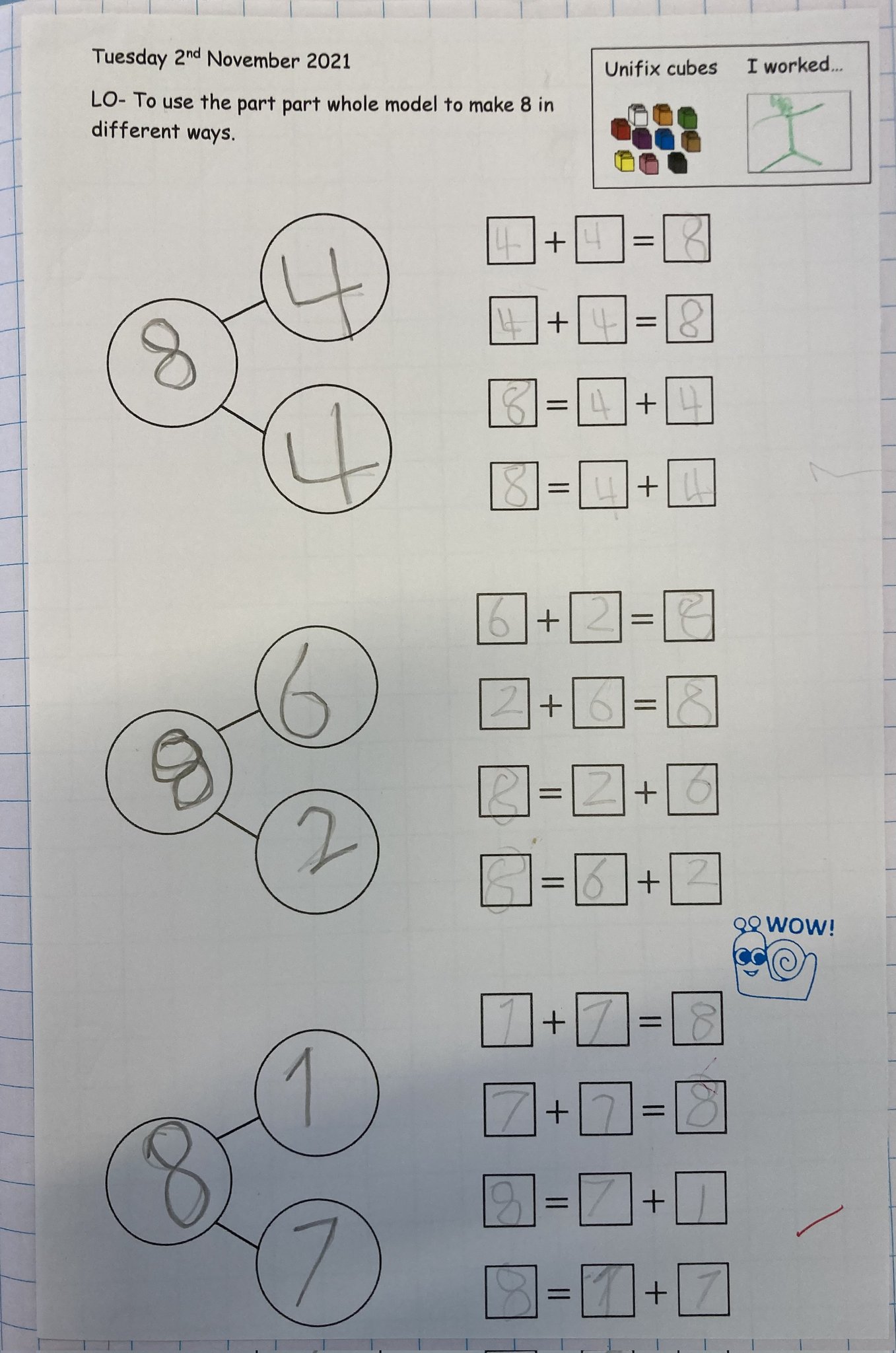
The CPA approach in year 1

Numicon in Reception
Intent
The study of mathematics enables the development of pupils’ natural ability to think logically and solve puzzles and real-life problems. Pupils learn to think creatively and make links between mathematical concepts through exploring patterns in the number system, shape, measures and statistics. They make and discuss propositions, explaining their reasoning and justifying their answers. They develop the skills, knowledge and efficient methods of calculation necessary to support their economic future and problem-solving in life.
Mathematics gives children a way of coming to terms with their environment. Practical tasks and real-life problems can be approached from a mathematical point of view. Mathematics provides children with imaginative areas of exploration and study and gives them the materials upon which to exercise their mathematical skills.

The national curriculum for mathematics aims to ensure that all pupils:
- become fluent in the fundamentals of mathematics, including through varied and frequent practice with increasingly complex problems over time, so that pupils develop conceptual understanding and the ability to recall and apply knowledge rapidly and accurately
- reason mathematically by following a line of enquiry, conjecturing relationships and generalisations, and developing an argument, justification or proof using mathematical language
- can solve problems by applying their mathematics to a variety of routine and non-routine problems with increasing sophistication, including breaking down problems into a series of simpler steps and persevering in seeking solutions
In addition to the overarching aims of the national curriculum, we at Abacus strive for pupils to:
- be positive and enthusiastic towards mathematics, with an awareness of the diversity of the subject
- be competent and confident in taking risks to apply mathematical knowledge, concepts and skills
- be able to work independently and in cooperation with others
- be able to use and apply mathematics across the curriculum, and to understand the application of mathematics in real life contexts and scenarios
At Abacus, we believe that children should leave primary education as confident, resilient mathematicians with a deep conceptual understanding of the skills required to approach any maths problem. Our mission is to enable all learners to enjoy and succeed in mathematics. We want learners to think about maths beyond what is tested in national examinations and to be equipped with an understanding of mathematics that will be relevant and useful in their future studies and in the world of work. We understand that a deep grasp of mathematics is essential to enabling greater social equity and mobility.
We want our pupils to be successful not only in their schooling career, but throughout their adult lives. Through carefully designed lessons, our teachers are able to make meaningful connections between content with a high emphasis placed on problem-solving. Our curriculum provides learners with a deep conceptual understanding of mathematical principles, the ability to confidently communicate in precise mathematical language, while becoming mathematical thinkers.
Implementation
To ensure whole-school consistency and progression, Mathematics at Abacus is planned and sequenced using a combination of the National Curriculum, White Rose and the Singapore Methods. New concepts are shared within the context of an initial related problem or ‘Big Picture’, which children are able to discuss in partners. This initial problem-solving activity prompts discussion and reasoning, as well as promoting an awareness of maths in relatable real-life contexts that link to other areas of learning. In EYFS, KS1 and KS2, these problems are almost always presented with objects (concrete manipulatives) and pictorial representations. Independent work provides the means for all children to develop their fluency further, before progressing to more complex related problems. Mathematical topics are taught in blocks, to enable the achievement of ‘mastery’ over time. Practice and consolidation play a central role. Carefully designed variation within this builds fluency and understanding of underlying mathematical concepts.
Please see the attachments to see the yearly overviews for each year group or for a more detailed breakdown of each maths topic, click the links that take you directly to the White Rose website. Please note that we do not follow this explicitly as a scheme of learning, but adapt it to the needs of our pupils and to sit alongside the topics we teach in other curriculum areas.
https://whiterosemaths.com/resources?year=year-1-new
https://whiterosemaths.com/resources?year=year-2-new
https://whiterosemaths.com/resources?year=year-3-new
https://whiterosemaths.com/resources?year=year-4-new
Impact
Assessment
Teachers use formative assessment strategies within maths lessons to assess and support learners. Children at Abacus have 4 dedicated whole class maths sessions per week, along with two additional 'maths meetings' each week dedicated to mental arithmetic skills. Children work in maths books and receive feedback through live marking and teacher feedback, peer and self-marking and discussion.
Children in years 2 and 6 complete statutory SATS maths tests in May. In addition to this, we support teacher judgement with termly maths 'quizzes' from year 1 upwards used to get children used to the style of maths tests in a fun and supportive way.
THRIVE-ing in maths
"We like learning about teen numbers. We’ve been writing them on our white boards." - Reception pupil.
"When we get stuck in Maths, we keep trying and don’t give up! If you still need help, you can ask the teacher and they will show you again." - Reception pupil.
"Our maths toolkits help us to remember more and we use actions so they stick!" - Year 2 pupil.
"Maths is fun. I love learning how to add and subtract using the column method." - Year 3 pupil.
"Relating our maths to every-day life helps us to remember it." - Year 4 pupil.
"Linking our maths topics helps us to learn, for example fractions, decimals and percentages." - Year 5 pupil.
"I love Maths because we are given the choice to learn a review if we need it or move onto a challenge page." - Year 6 pupil.
"We learn rhymes or mnemonics to help us remember key facts like BIDMAS." - Year 6 pupil.
Here at Abacus, we base our curriculum on the Singapore Maths approach. Through our involvement with Maths hubs, as well as first-hand visits to schools in Singapore, we have written a unique curriculum which encourages mastery and fluency in Mathematics.
What is Mastery?
At Abacus we believe that all children benefit from deepening their conceptual understanding of mathematics. Children here are given the time to investigate and explore new mathematical concepts rather than accelerating through topics at a pre-determined pace. By affording children more time to cover key concepts in greater depth, they fully grasp new learning and become more flexible, independent mathematicians.
CPA
Children and adults can find maths difficult because it is abstract. The CPA approach helps children learn new ideas and build on their existing knowledge by introducing abstract concepts in a more familiar and tangible way.
C (Concrete)
Children are first introduced to a new concept or skill by acting it out with real objects such as cubes or counters.
P (Pictorial)
When children have had hands on experience they are ready to relate the problem to pictures or diagrams.
A (Abstract)
The most mysterious or abstract stage uses mathematical notation such as digits and symbols. We so easily jump to this last step but this can be very abstract without practical hands on experiences.
These three stages should run alongside each other as much as possible to provide ‘depth not breadth’ and make links between new and prior learning. An example (from our calculation policy) is provided below.
/B3F9C56579641FBFCAA34F94484F9AF6.jpg)
Growth Mindset
We believe that children’s abilities are not fixed but can be developed through practice, support, dedication and hard work. This belief encourages a love of learning and resilience that enables everyone to achieve and we are proud to champion this ethos in everything that we do at abacus.
What Can I do to Help my Child at Home?
Use real objects or represent number in pictures alongside digits and symbols wherever possible to enrich your child’s understanding.
Provide real life experiences of maths wherever possible, such as handling change in the shop, talking about shapes in the environment, numbers on buses, phone numbers… Maths is all around us!
Find below a list of useful websites, many of which are free, others offer a free trial.
nrich.maths.org/frontpage
ictgames.com
mathszone.co.uk
busythings.co.uk
kangaroomaths.com
snappymaths.com
bbc.co.uk/education







